introduction Link to heading
Convolution, a versatile mathematical operation, has become a go-to tool in various domains, from image processing to Deep learning. However, its roots trace back to its initial application in system analysis and this blog is my attempt on explaining the premise as to why was convolution required in the first place and the thought process on how it was developed
modelling systems Link to heading
- Think of a system as any device or setup that changes or controls something. An amplifier boosts sound, a spring bounces, and cruise control keeps your car’s speed steady – all systems!
- we also assume that any system we are going to deal with here is linear and time invariant for easier analysis and modelling
linear: Twice the input gives twice the output
time invariant: Delaying the input delays the output, say the input to a sound recorder is delayed even the output is delayed by equal amount
PROBLEM Link to heading
- now after modelling a system it is a necessity to test the system for all sorts of inputs but doing so manually is way too time consuming
- a real life exmaple of what Is meant by the above statement is given below
Step input: A sudden change in desired altitude, testing the system’s ability to quickly reach and stabilize at a new height.
Ramp input: A gradual increase or decrease in desired altitude, evaluating the system’s tracking performance and smoothness.
Sinusoidal input: A periodic wave-like change in desired altitude, assessing the system’s ability to handle oscillations and resonant
frequencies.
Random input: A series of unpredictable altitude changes, simulating real-world disturbances and testing robustness.
PREREQUISITE (THE MAGIC FUNCTION) UNIT IMPULSE FUNCTION Link to heading
Think of the Impulse signal as a short pulse with amplitude being infinity at t=0 b
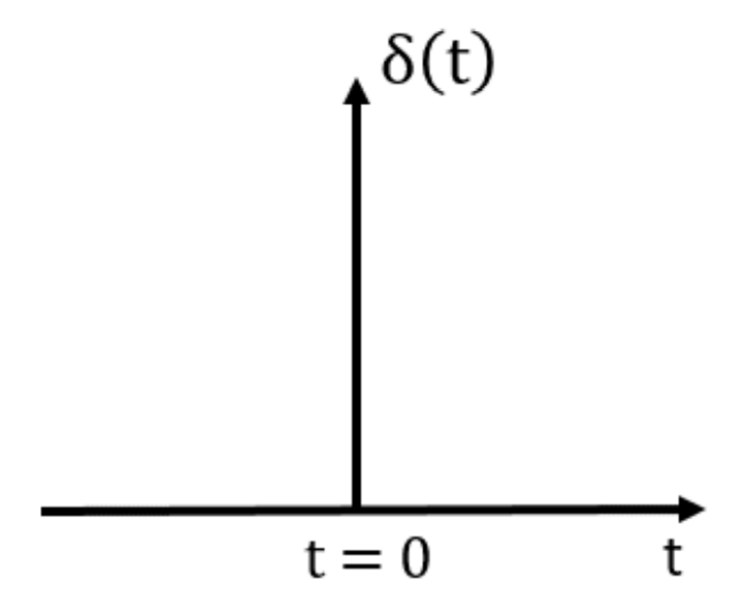
At t = 0: δ(t) = ∞ (infinite value at t = 0)
At t ≠ 0: δ(t) = 0 (zero for any other value of t)
but why is it called Unit Impulse function in the first place ?? The name comes from the fact that the area of an impulse function is one
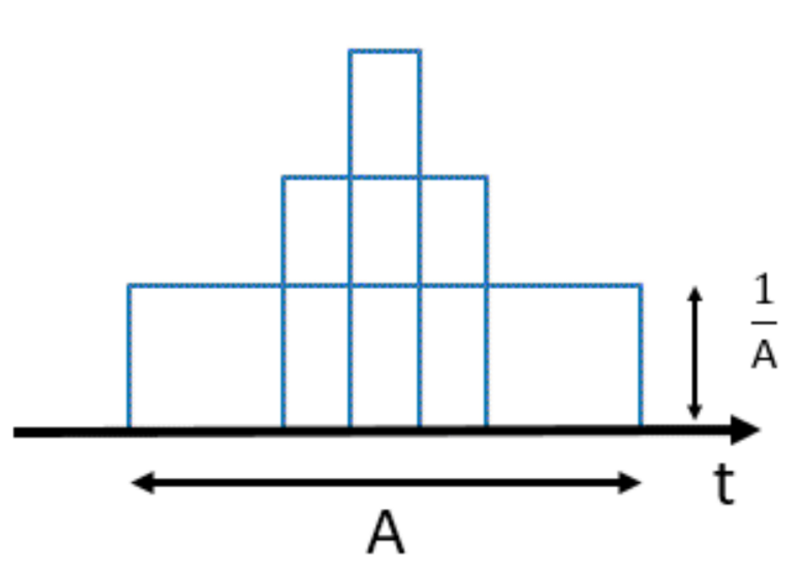
Reason behind area being 1
Consider a narrow rectangular pulse of width A and height 1/A, so that the area under the pulse = 1. Now if we go on reducing the width A and maintain the area as unity, then the height 1/A will go
on increasing. Ultimately when A=0, 1/A=infinity and this results in a pulse of infinite magnitude. It is very clear from this, that the Unit impulse function has infinite magnitude at t = 0
SOLUTION Link to heading
now why did we need to know about this function what is so special about it this can be better understood by the image below
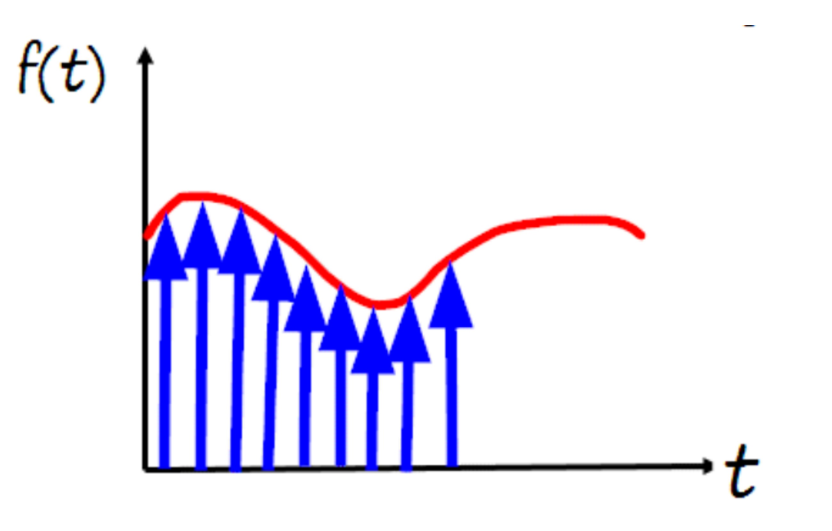
- Figured it out yet? In the second figure shown above, we have substituted the signal in the first figure, by infinite number of Impulses of appropriate magnitudes at each instant of time. In this manner, any signal can be constructed out of scaled and shifted Unit Impulse signals.
- By figuring out how the system responds to a Unit Impulse signal, we can predict the system response to any input signal. The response of a system to a Unit Impulse signal is called the Unit Impulse Response (denoted by h(t))
- Because these are LTI systems, the output is scaled and shifted by the same factor as the input Impulse signal. So the output to any input can be obtained by summing up the scaled and shifted outputs(impulse response’s)
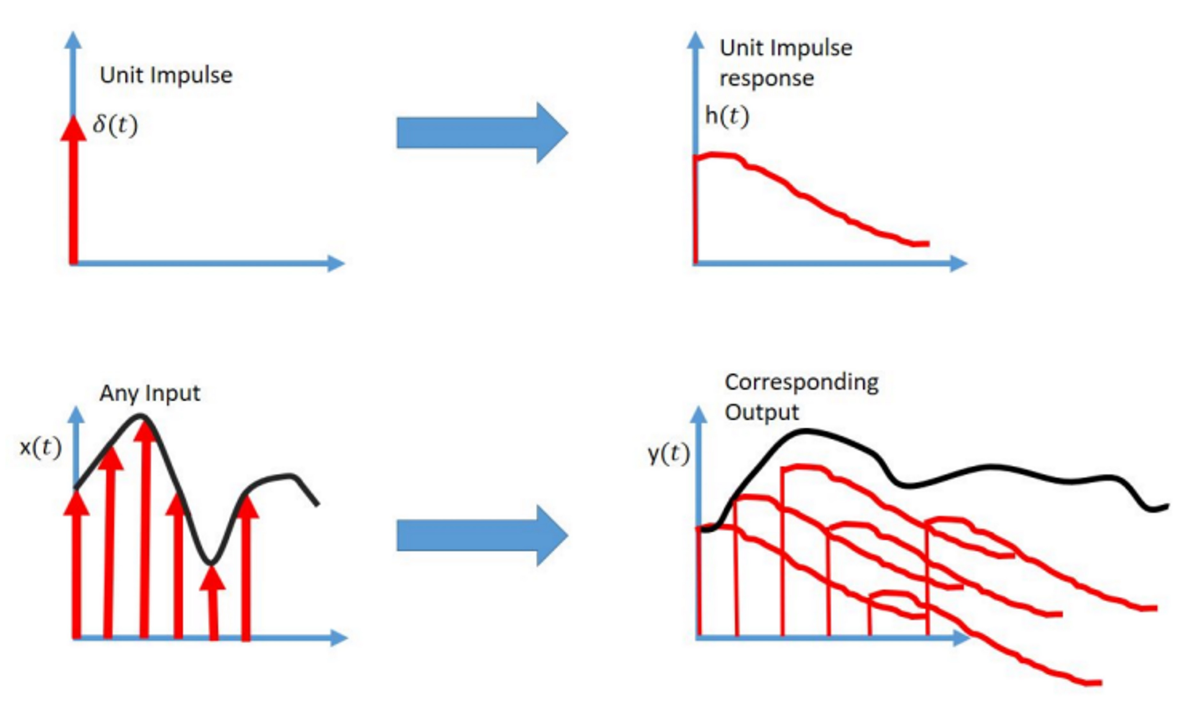
now to sum up these infinite scaled and shifted impulse responses means we multiply the amplitude of the input x(tau) with the shifted output h(t-tau) and integrate it where tau varies negative infinity to positive infinity as the input signal is made of infinite impulse signals
and woila we get the convolution operation
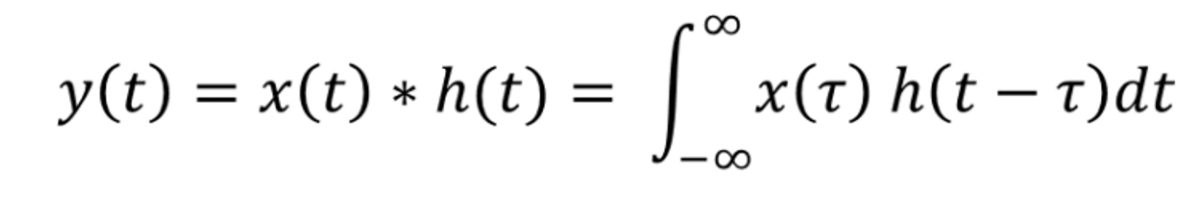
it’s a wrap
thanks for reading out till the end and I hope i was able to make convolution a little more intuitive
Adiós!